개발놀이터

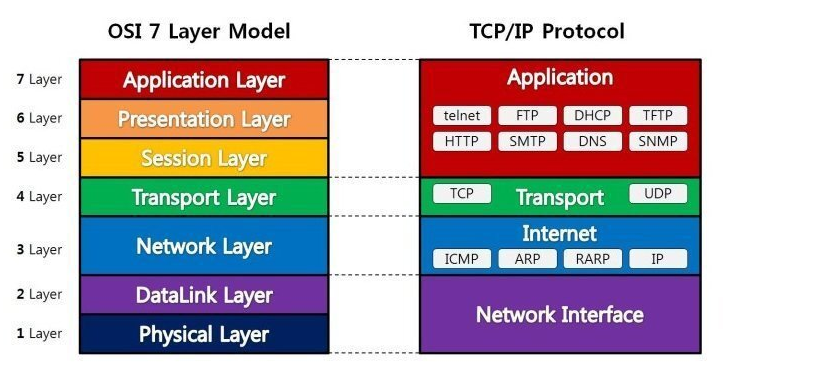
네트워크를 공부할 때 OSI 7계층이나 TCP 4계층에 대해서 들어본적이 있을겁니다. 우리는 이번 포스팅에서 OSI 7계층, TCP 4계층이 무엇인지, 이 둘의 차이는 무엇인지, 이 계층을 알면 뭐가 좋은지에 대해서 알아보도록 하겠습니다. 우선 포스팅에 들어가기 앞서 OSI 7계층과 TCP 4계층은 크게 다르지 않다는 것을 말씀드리고 시작해보겠습니다. OSI 7계층 OSI 7계층과 TCP 4계층을 그림으로 나타내면 다음과 같습니다. 우선 OSI 7계층이 뭔지 알아야겠죠? OSI는 Open System Interconnection의 약자입니다. 이름만 봐도 대충 어떤 느낌인지 알것 같습니다. OSI 모델은 컴퓨터 시스템이 네트워크위에서 의사소통을 위해 사용되는 일곱개의 층입니다. 즉 OSI 7계층은 네트워..

configure : 구성하다 / 배열하다 / 설정하다 evident : 분명한, 명백한 transitive : 의존적인 / 의지하는 / 타자의 동작을 이행하는 include : 포함하다 / 내포하다 optimization : 최적화 comes with : ~와 함께 제공된다. fetch : 가지고 오다 / 의식을 회복시키다 / 설득하다 explicit : 명시적 allow : 허락하다, 묵인하다 / (정기적으로) 지급하다 / 인정하다 / 참작하다 compromised : 타협하다 integrity : 고결, 성실, 청렴 / 완전한 상태 demarcate : 분리하다, 구별하다 compelling : 강제적인 / 흥미를 돋우는 / 어쩔 수 없는 At the most basic level, a connec..

이번 포스팅에서는 트랜잭션과 ACID 그리고 더 나아가서 자바에서 트랜잭션을 어떻게 다루는지에 대해서 알아보도록 하겠습니다. 굉장히 딥하게 들어가기 때문에 트랜잭션과 ACID에 대한 기본적인 내용에 대해서만 알고싶으신 분들은 앞부분만 읽으시고 뒷부분은 알아만 두시는 것을 추천드리겠습니다. 최대한 쉽게 풀어서 쓸거라 찬찬히 읽으시면 이해가 안되지는 않을겁니다! 그럼 시작해보죠 트랜잭션 트랜잭션을 간단하게 한마디로 설명하자면 "데이터베이스의 상태를 변경시키기 위한 논리적인 단위" 라고 할 수 있습니다. 여기서 상태를 변경시킨다는 것은 우리가 흔히 사용하는 SQL문을 이용한 것입니다. DDL, DML등을 말하는 것이지요. 트랜잭션에 대한 개념은 이게 다입니다. 조금 허무하시죠? 이제 트랜잭션의 특징이라고 말할..

이번 포스팅에서는 커넥션 풀에 대해서 알아보도록 하겠습니다. 커넥션 풀링은 데이터 접근 패턴으로 많이 알려져있습니다. 커넥션 풀링은 데이터베이스 커넥션과 읽고/쓰는 데이터베이스 작업 성능을 포함되는 과부하를 줄이기위한 목적으로 사용됩니다. 기본적인 레벨에서 커넥션 풀은 데이터베이스 커넥션 캐싱 구현체입니다. 이것은 개발자들의 특별한 요구를 적절하게 구성할 수 있습니다. 커넥션 풀 왜 커넥션 풀을 사용해야 할까요? 이 질문에 대한 답을 얻기 위해서는 데이터베이스가 커넥션 작업을 하는 동안 벌어지는 일에 대해서 알면 답할 수 있습니다. 데이터베이스 커넥션은 데이터베이스 드라이버를 사용해서 커넥션을 엽니다. 읽기/쓰기에 의해 생성된 데이터를 위해 TCP 소켓을 엽니다. 읽기/쓰기에 의해 생성된 데이터를 소켓에..

exceed : 초과하다 abbreviate : 단축하다, 생략하다 attempt : 시도하다 / 기도하다 / 꾀하다 retrieval : 회복, 복구, 만회 / 수정 / 사전에는 안나오지만 검색이라는 뜻도 있음 alleviate : 덜다, 완화하다 vastly : 대단히 크게 we should favor the Deque interface and its implementations. 우리는 Deque의 인터페이스와 Deque의 구현체들을 주로 사용해야합니다. favor : 선호하다 / 호의 -> 대충 의역했는데 아무리봐도 선호하다나 호의로 해석하면 이상하단 말이지... First, we'll take a peek at what a Queue does, and some of its core methods..

preserve : 보호하다 / 보존하다 / 지키다 descendant : 자손 / 후예 incur : 초래하다 / 지다 (빚을 지다) represent : 의미하다 / 나타내다 / 대표하다 propagation : 번식, 증식 / 전파 comprise : 포함하다 / 의미하다 / 구성되다 The LinkedHashSet saves the client from the unpredictable ordering provided by HashSet, without incurring the complexity that comes with a TreeSet. HashSet에 의하여 제공된 예측불가능한 순서로부터 클라이언트(개발자)를 보호한다. TreeSet과 같은 복잡성을 초래하지 않으면서 의역 -> TreeSe..

Maps are naturally one of the most widely style of Java collection Map은 기본적으로 Java Collection 중 가장 대중적인 것 중 하나이다. And, importantly. HashMap is not a thread-safe implementation. while Hashtable does provide thread-safety by synchronizing operations. 그리고 중요하다. Hashtable은 synchronizing 동작을 이용해 thread-safety 한 반면에 HashMap은 thread-safe 하지 않은 구현체이다. Even though Hashtables is thread safe. it is not ver..

이번 포스팅에선 스택의 오랜 친구인 Queue (이하 큐)에 대해서 알아보는 시간을 가져보겠습니다. 우선 이번 포스팅에서는 큐에 대한 개념과 핵심 메서드에 대해서 알아보고, 그 이후에는 자바에서 제공하고 있는 구현체에 대해서 알아보고 마지막으로 큐가 thread-safe한지에 대해서 알아보겠습니다. Queue 자바에서 큐는 일반적인 도로와 같은 느낌입니다. 제일 먼저 들어온 것이 제일 먼저 나가는 구조이지요. 이것을 FIFO (First In First Out)라고 부릅니다. 큐의 일반적인 느낌은 위와 같습니다. 핵심 메서드 큐는 인터페이스인데요. 큐를 구현하는 모든 구현체들은 아래의 세가지 핵심 메서드를 포함해야합니다. offer() : 큐의 뒤쪽에 새로운 값을 삽입합니다. poll() : 큐의 앞쪽에..

이번 포스팅에서는 자료구조 중 가장 유명하다고 해도 과언이 아닌 스택에 대해서 알아보도록 하겠습니다. Stack 스택은 가장 전형적인 LIFO (Last In First Out) 구조로서 개발자들에게 사랑받는 자료구조 중 하나입니다. 스택이 사용되는 것은 가장 대표적으로 홈페이지의 뒤로가기 버튼과 ctrl + z인 undo 기능 계산기의 계산알고리즘 등이 있습니다. 하지만 요즘은 스택을 사용하기 보단 Deque (이하 데크)를 사용하는 것을 더 추천하긴 합니다. Deque는 Double Ended Queue의 약자로 상황에따라 해당 컬렉션을 스택으로 쓸 수도 큐로 쓸 수도 있는 인터페이스입니다. 데크는 LIFO 실행에 있어서 더 완벽하고 일관성있기 때문에 최근에는 스택 대신 사용하게 되었습니다. 하지만 ..

우리는 이전 시간 RESTful API에 대해서 알아봤습니다. 그리고 크리티컬한 단점인 유연하지 못하다는 특징에 대해서도 잠깐 알아봤죠. RESTful이 유연하지 못하다는 것은 앞서 설명했듯이 요구사항이 계속 추가될 때마다 새로운 API를 만들어야 한다는 것도 있지만 Over Fetching, Under Fetching 이 두가지 문제도 큰 문제 중 하나입니다. 이번 포스팅에서는 RESTful API가 가진 한계에 대해 자세히 알아보고 그 대안책으로 나온 GraphQL에 대해 자세히 알아보도록 하겠습니다. RESTful API의 한계 REST API의 한계는 너무 명확합니다. 요구사항이 추가될 때마다 새로운 API를 만들어야 하기 때문에 유지보수가 장난아니게 힘들다는 점이 크리티컬했죠. REST API는..