시간복잡도
시간복잡도란 내가 만든 코드가 얼마나 효율적인지를 나타내는 척도입니다. 시간복잡도를 계산하면 코드의 어느 부분에서 시간을 많이 잡아먹고 있는지 대략적으로 알 수 있으며 코드를 리팩토링 할 때도 좋은 영향을 미칠 수 있습니다.
문제를 해결하기 위한 알고리즘의 로직을 코드로 구현할 때 시간 복잡도를 고려한다는 것은 무슨 의미일까요?
바로 '입력값의 변화에 따라 연산을 실행할 때, 연산 횟수에 비해 시간이 얼마나 걸리는가?'를 고려한다는 의미입니다.
효율적인 알고리즘을 구현한다는 것은 바꾸어 말해 입력값이 커짐에 따라 증가하는 시간의 비율을 최소화한 알고리즘을 구성했다는 의미입니다.
그리고 이 시간복잡도는 빅-오 표기법을 사용해 나타냅니다.
빅-오 표기법
빅-오 표기법 말고도 빅-오메가 표기법, 빅-세타 표기법이 있지만 많이 사용하지 않습니다.
왜냐하면 빅-오 표기법은 최악의 상황을 가정하고 계산한 시간이고 빅-오메가는 최선의 상황을 가정하고 계산한 시간, 빅-세타는 평균값을 가정하고 계산한 시간이기 때문입니다.
최선의 상황과 평균의 상황을 가정하게 되면 자칫 계산한 값과 결과가 다르게 나왔을 경우 어디에서 문제가 발생했는지 쉽게 발견하지 못할 수도 있습니다.
따라서 최악의 상황을 가정하는 빅-오 표기법이 대중적으로 많이 사용되는 표기법입니다.
그럼 빅-오 표기법에 대해서 바로 알아보도록 하죠
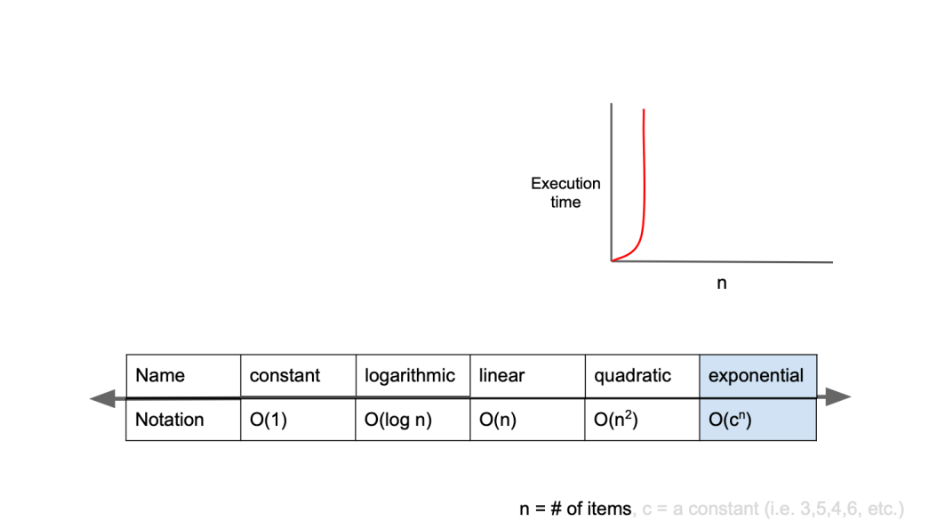
빅-오 표기법의 종류는 다음과 같습니다.
- O(1)
- O(log n), O(nlog n)
- O(n)
- O(n^2)
- O(2^n)
- O(n!)
n을 무한대로 보냈을 때 그래프는 다음과 같습니다.

이제 각각의 경우를 코드와 함께 살펴보면서 대충 어떤 느낌인지 보도록 하겠습니다.
O(1)

O(1)은 일정한 복잡도라고 하며, 입력값이 증가하더라도 시간이 늘어나지 않습니다.
function O_1_algorithm(arr, index) {
return arr[index];
}
let arr = [1, 2, 3, 4, 5];
let index = 1;
let result = O_1_algorithm(arr, index);
console.log(result); // 2이 알고리즘에선 입력값이 크기가 아무리 커져도 즉시 출력값을 얻어낼 수 있습니다.
예를 들어서 arr의 길이가 100만이더라도, 즉시 해당 index에 접근해 값을 반환할 수 있습니다. 가장 시간이 적게 드는 가장 효율적인 알고리즘으로서 이렇게 만들수만 있다면 가장 지향해야하는 방식입니다.
O(logn), O(nlogn)

O(log n)은 로그 복잡도라고 부르며, 빅-오 표기법중 O(1) 다음으로 빠른 시간 복잡도를 가집니다.
주로 입력 크기에 따라 처리 시간이 증가하는 정렬알고리즘에서 많이 사용됩니다.
알고리즘중에 유명한 BST (Binary Search Tree / 이진 검색 트리) 또한 O(log n) 의 시간 복잡도를 가지고 있습니다.
간단하게 BST에 대해서 예시를 통해 설명하자면,

이런 트리가 있다고 가정하겠습니다. 우리는 이 트리에서 5를 찾아야합니다.
만약 이걸 for 문으로 돌리기 시작하면 최악의 경우 O(2^n)의 시간복잡도를 가집니다. (정확히는 O(2^(n-1)))
2진 탐색 트리에서는
1. 루트 노드의 키와 찾고자 하는 값을 비교한다. 찾고자 하는 값이라면 탐색을 종료한다.
2. 찾고자 하는 값이 루트 노드의 키보다 작다면 왼쪽 서브 트리로 탐색을 진행한다.
3. 찾고자 하는 값이 루트노드의 키보다 크다면 오른쪽 서브트리로 탐색을 진행한다.
이러한 알고리즘에 의해 값을 찾게됩니다.
그렇게 해서 결국

이러한 방식으로 5를 찾아낼 수 있게 되는 것이죠.
이처럼 입력 값이 점점 커지게 되는 상황에서 이진탐색트리 알고리즘을 사용하게 되고 위와 같은 상황에서 최악의 경우 입력값이 7개인 상황에서 단 세번의 계산만으로 원하는 값을 찾아낼 수 있습니다.
그런데 여기서 의문이 들 수 있습니다.
원하는 값이 5고 첫번째 값이 7인데 5가 왼쪽이 아니고 오른쪽 두번째에 있으면 그게 더 빠른건데 오른쪽으로 가지않고 굳이 값이 작으면 왼쪽으로 가는 이유는 무엇일까요?
그것은 제가 생각했을 때 물론 5가 오른쪽 두번째에 있을 때 오른쪽으로 가는게 가장 빠르겠지요 하지만 그건 오른쪽이 아니고 왼쪽에 5가 있는 경우에도 마찬가지입니다.
따라서 노드를 전부 뒤지는 최악의 상황을 피할 수 있다는 것 만으로도 이진탐색트리는 훌륭한 해결책이 될 수 있습니다.
O(n)

O(n)은 선형 복잡도라고 부르며, 입력값이 증가함에따라 시간 또한 같은 비율로 증가하는 것을 말합니다.
예를 들어서 입력값이 1일 때 1초가 걸리고, 입력값을 100배 증가시켰을 때 1초의 100배인 100초가 걸리는 알고리즘을 구현했다면, 그 알고리즘은 O(n)의 시간복잡도를 가진다고 할 수 있습니다.
function O_n_algorithm(n) {
for (let i = 0; i < n; i++) {
// do something for 1 second
}
}
function another_O_n_algorithm(n) {
for (let i = 0; i < 2n; i++) {
// do something for 1 second
}
}입력값이 1 증가할때마다 코드의 실행시간이 2초씩 증가합니다.
그럼 이것을 보고 O(2n) 이라고 볼 수도 있지만 시간복잡도를 계산할때는 n이 무한대로 커진다고 (최악의 상황이라고) 가정하기 때문에 2n 과 n 은 무한대로 가면 결국 의미가 퇴색되게 됩니다.
따라서 위의 경우에는 O(n) 이라고 표기하는 것이 올바른 표기입니다.
O(n^2)

O(n^2)은 2차 복잡도라고 부르며, 입력값이 증가함에 따라 시간이 n의 제곱수의 비율로 증가하는 것을 의미합니다.
예를 들어 입력값이 1일 경우 1초가 걸리던 알고리즘에 5라는 값을 주었더니 25초가 걸리게 된다면, 이 알고리즘의 시간 복잡도는 O(n^2) 라고 표기합니다.
대표적으로 2중 for문을 들 수 있겠는데요
function O_quadratic_algorithm(n) {
for (let i = 0; i < n; i++) {
for (let j = 0; j < n; j++) {
// do something for 1 second
}
}
}
function another_O_quadratic_algorithm(n) {
for (let i = 0; i < n; i++) {
for (let j = 0; j < n; j++) {
for (let k = 0; k < n; k++) {
// do something for 1 second
}
}
}
}이렇게 2중으로 for문이 돌면 시간 복잡도가 O(n^2)만큼 소요가 됩니다.
O(2^n)
O(2^n)은 기하급수적 복잡도라고 부르며, 빅-오 표기법 중 가장 느린 시간 복잡도를 가집니다. (물론 이론상 O(n!) 이 가장 느리긴 하지만 n! 은 현실세계에서 존재하지 않는다고 봐도 될정도로 적은 시간복잡도입니다.)
만약 구현한 알고리즘이 O(2^n)의 시간복잡도를 가진다면 다른 방법을 고민해보는 것이 좋을 것 같습니다.
function fibonacci(n) {
if (n <= 1) {
return 1;
}
return fibonacci(n - 1) + fibonacci(n - 2);
}
대표적인 O(2^n) 시간복잡도를 가진 알고리즘은 바로 피보나치 수열을 재귀로 구현하는 방식입니다. 해당 알고리즘을 브라우저 개발창에서 n을 40으로 두어도 수초가 걸리는 것을 확인할 수 있으며, n이 100이상이면 평생 결과를 반환받지 못할 수도 있습니다.
여기서 포스팅을 마쳐도 좋겠지만 저는 개인적으로 여기까지 구글링을 통해 알아봤을 때 뭔가 아쉬웠습니다.
시간 복잡도를 직접 계산하는 방법은 없나?
그리고 아주 간단한 구글링으로 시간 복잡도를 직접 계산할 수 있는 방법을 찾았습니다.
만약 저처럼 학생이거나 신입으로 회사에 들어가는 경우 코딩테스트를 본 뒤에 코드리뷰를 하면서 시간복잡도를 구해보라는 질문을 받을 수 있습니다. (면접 후기를 몇개 봤을 때 해당 질문이 많았습니다.)
그래서 시간 복잡도를 직접 계산해 봅시다.
int sum = 0;
for (int i = 0; i < n; i++) {
sum += i;
}
-----------------------------
int sum = (n + 1) * n / 2;위 아래로 나뉜 이 코드는 입력받은 n 만큼 합을 구하는 코드입니다.
위의 방식은 for 문을 통해 하나하나 다 더한 방식이고 아래의 코드는 흔히 알려진 n까지 합을 구하는 공식을 사용한 모습입니다.
먼저 위의 코드에서 sum = 0이 한번 계산되고 i = 0이 한번, i++가 n번, sum += i 가 n번 계산되어 총 2n + 2 번만큼 계산되었습니다. 이것을 빅-오 표기법에 넣어보면 O(2n-2)가 되는데 위에서도 말했듯이 n이 무한대로 가면 의미가 퇴색되기 때문에 이는 O(n)으로 표기 가능합니다.
아래의 방식도 살펴볼까요?
n + 1이 한번, * n 이 한번, / 2 가 한번 총 세번 연산이 들어갔습니다. 이는 빅-오 표기법으로 O(3)이며 이는 O(1)과 같습니다.
어떤가요? 같은 합을 구하는 공식이지만 한쪽은 O(n)으로 빠른편은 아니지만 O(1)은 빅-오 표기법에서 사용할 수 있는 모든 시간복잡도중에 가장 빠른 속도로 구현 가능합니다.
이렇듯 알고리즘을 조금씩 수정하는 것으로 성능향상을 불러일으킬 수 있습니다.
조금 복잡한 예제로 확인해보겠습니다.
int sum = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < i; j++) {
sum += j;
}
}
위의 코드는 2중 for 문으로써 직접 계산해보면 sum = 0이 한번, i++이 n번 j++이 i번(n번), sum += j 가 0, 1, 2, 3,....(n-1)번 반복되어 총 1 + n + n(n-1) 번 반복되어 총 O(n^2)의 시간복잡도를 가집니다.
여기까지 알고리즘, 자료구조에서 가장 기초적인 시간복잡도에 대해서 알아봤습니다. 이번에 알고리즘 공부를 하면서 처음 보게된 단어인데 막상 공부해보니 그렇게까지 어렵지는 않네요
여기까지 긴 글 읽어주셔서 감사합니다. 좋은하루 보내세요~
출처
시간 복잡도
[알고리즘] Time Complexity (시간 복잡도) - 하나몬
⚡️ Time Complexity (시간 복잡도) Time Complexity (시간 복잡도)를 고려한 효율적인 알고리즘 구현 방법에 대한 고민과 Big-O 표기법을 이용해 시간 복잡도를 나타내는 방법에 대해 알아봅시다. ❗️효
hanamon.kr
이진 검색 트리 예제코드
https://blog.chulgil.me/algorithm/
알고리즘의 시간 복잡도와 Big-O 쉽게 이해하기
삼성역에서 택시를 타고 강남역으로 향했는데 30분 걸렸다. 구글에서 알려주는 최단경로로 갔더라면 15분내에 도착할 것이다. 레스토랑을 예약해서 가는 경우라던지 친구와 약속시간을 잡은경
blog.chulgil.me
이진 검색 트리
https://code-lab1.tistory.com/10
[자료구조] 이진탐색트리(Binary Search Tree)의 개념, 이해 | C언어 이진탐색트리 구현
이진탐색트리(Binary Search Tree)이란? 이진탐색트리란 다음과 같은 특징을 갖는 이진트리를 말한다. ( #이진트리 - 각 노드의 자식 노드가 최대 2개인 트리) 1. 각 노드에 중복되지 않는 키(key)가 있다
code-lab1.tistory.com
시간 복잡도 직접 계산하기
코드의 시간 복잡도 계산하기
안녕하세요. 저는 휴먼스케이프 인턴 Jason입니다.
medium.com
'CS 지식 > 자료구조, 알고리즘' 카테고리의 다른 글
| 자료구조 : Tree (0) | 2023.02.23 |
|---|---|
| 자료구조 : Hash (0) | 2023.02.23 |
| 자료구조 : Map (0) | 2023.02.18 |
| Two-Pointers-Algorithm (0) | 2023.02.15 |
| 에라토스테네스의 체 (소수 구하기) (0) | 2023.02.14 |