이번 시간에는 전 시간에 이어서 컴퓨터 사이언스에서 가장 사랑받는 자료구조 중 하나인 Tree에 대해서 알아보도록 하겠습니다.
이번 포스팅에서는 Tree의 개념, Tree 구조에서 가장 많이 사용하는 구조인 이진 트리, 이진 탐색 트리에 대해서 알아보도록 하겠습니다.
Tree
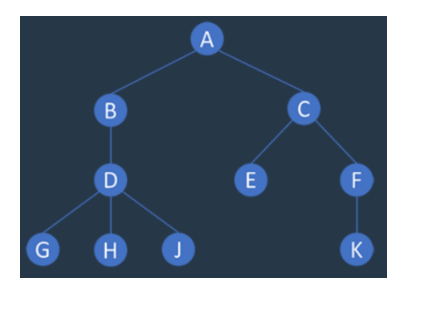
트리의 구조는 위의 사진과 같습니다. 나무가 가지를 뻗듯이 데이터를 저장한다고 하여 붙여진 이름이 바로 트리입니다.
트리의 이러한 구조는 데이터의 저장보다는 저장된 데이터를 효과적으로 탐색하기 위해서 사용합니다. 따라서 Heap Space가 트리로 구현되어 있고, 컴퓨터에서 디렉토리를 분류할 때에도 트리 구조를 사용합니다.
트리의 개념에 대해 알아봤으니 용어를 알아보도록 하겠습니다.
- 루트 노드 (root node) : 부모가 없는 최상위 노드
- 단말 노드 (leaf node) : 자식이 없는 최하위 노드(들)
- 크기 (size) : 트리에 포함된 모든 노드의 개수
- 깊이 (depth) : 루트 노드로부터의 거리
- 높이 (height) : 깊이 중 최댓값
용어도 크게 어려운게 없으니 빠르게 넘어가도록 하겠습니다.
트리 구조를 가장 효율적으로 사용하는 방법에는 이진 트리가 있습니다. 이제 이진 트리에 대해 알아볼까요?
이진 트리 (Binary Tree)

트리를 구성하는 노드의 가지 개수는 0개, 1개, 2개, 3개... 등 여러개가 될 수 있지만 이진 트리는 다릅니다.
이진 트리는 모든 노드가 최대 2개의 서브 트리를 가지고 있는 트리로, 서브 트리 또한 모두 이진트리입니다. 즉, 가지가 최대 2개인 노드로만 구서오디는 트리라는 뜻입니다.
이진 트리의 종류로는 편향 이진 트리 (Skewed Binary Tree), 포화 이진 트리 (Full Binary Tree), 완전 이진 트리 (Compelete Binary Tree) 이렇게 세가지 입니다. 각각에 대해서 알아볼까요?
편향 이진 트리 (Skewed Binary Tree)

편향 이진 트리는 하나의 차수로만 이루어져 있는 경우를 의미합니다. 이러한 구조는 배열(리스트)과 같은 선형 구조이므로 가장 아래쪽에 위치한 노드를 탐색하기 위해 모든 데이터를 전부 탐색해야 한다는 단점이 있어서 효율적이지 못합니다.
포화 이진 트리 (Full Binary Tree)
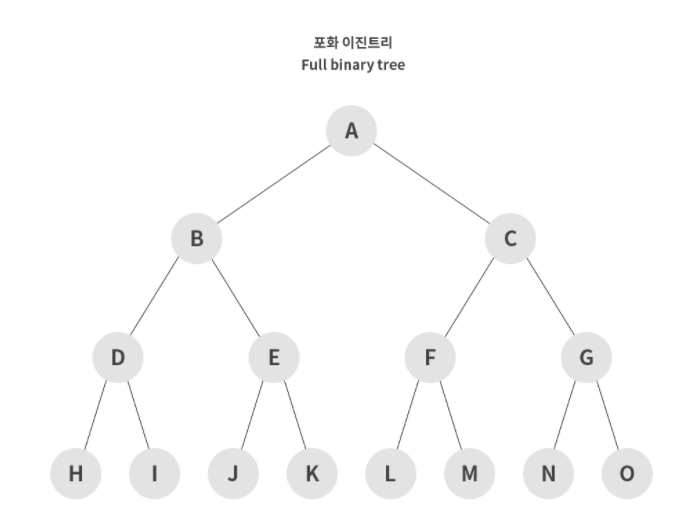
포화 이진 트리는 Leaf Node를 제외한 모든 노드의 차수가 2개로 이루어져 있는 경우를 의미합ㄴ디ㅏ. 이 경우 해당 차수에 몇 개의 노드가 존재하는지 바로 알 수 있으므로 노드의 개수를 파악할 때 용이한 장점이 있습니다.
완전 이진 트리 (Compelete Binary Tree)
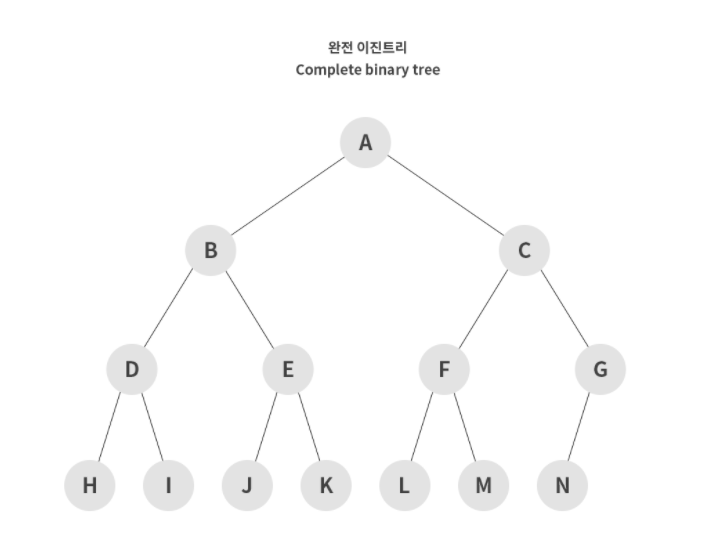
포화 이진 트리와 같은 개념으로 트리를 생성하지만, 모든 노드가 왼쪽부터 차근차근 생성되는 이진 트리를 의미합니다. Heap Space가 완전 이진 트리의 일종입니다.
이진 탐색 트리
이진 탐색 트리는 이진 트리의 일종이지만 조건이 붙어있는 트리입니다.
입력된 값과 노드를 비교하여 작은 값이면 왼쪽으로 큰 값이면 오른쪽으로 가서 저장됩니다.

위와 같이 이진 탐색 트리를 만들었습니다. 그런데 왜 이진 탐색 트리 형태로 만들까요? 바로 데이터를 효율적으로 탐색할 수 있기 때문입니다.
원하는 값을 찾을 때까지 현재의 노드값보다 찾고자하는 값이 작으면 왼쪽으로 움직이고, 크면 오른쪽으로 움직입니다. 이렇게하면 원하는 값을 더 빠르게 찾을 수 있습니다.
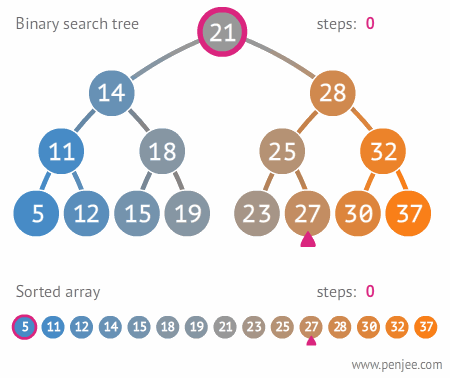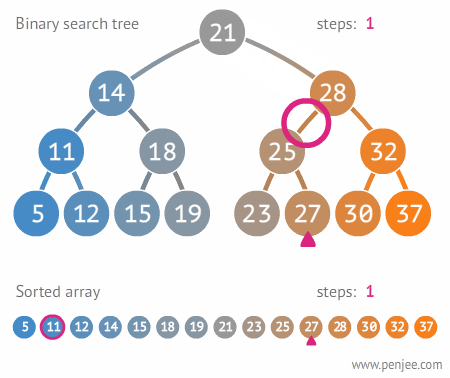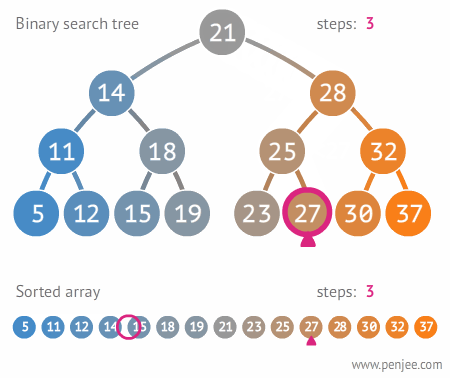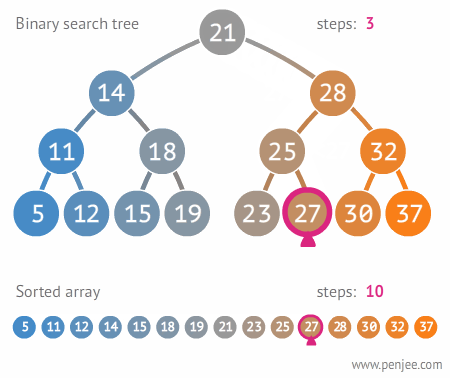
위의 예제는 위쪽은 이진 탐색 트리로 27을 찾는 과정이고 아래는 무작정 처음부터 27을 구하는 과정입니다. 이진 탐색 트리를 활용하면 3번만에 끝나는 과정이 배열이나 리스트로 찾게 되면 10번이나 됩니다.
이진 탐색 트리가 탐색에 용이하다는 것은 이제 알겠습니다. 하지만 이진 탐색 트리의 또 하나의 장점이 있죠 바로 정렬이 가능하다는 것입니다.
바로 위의 예제를 확인해보면
왼쪽 맨 아래서부터 ↗↘이렇게 값을 읽어나가면 다음과 같습니다.
5 11 12 14 15 18 19 21 23 ....
그래서 자바에서 Tree 자료구조를 이용한 대표적인 클래스인 TreeMap과 TreeSet이 이러한 방식으로 값을 정렬합니다. 트리 구조를 이용한 두개의 클래스는 들어오는 값이 어떤 값이던 간에 이진 탐색 트리의 조건에 맞게 배치하면 저절로 정렬이 되기 때문에 딱히 정렬에 특별한 로직을 사용하지 않아도 됩니다.
이진 탐색 트리의 시간 복잡도는 탐색, 저장 모두 O(log n)을 가집니다. Hash와 비교하면 성능상 이점을 보긴 힘들지만 정렬에 대한 이점과 key 값을 모를 때 값을 처음부터 찾아나가야 한다면 Tree 구조를 사용하는 클래스들이 나쁘지만은 않습니다.
또한 시간 복잡도가 O(log n)은 코딩테스트에서 웬만하면 시간 초과가 뜨지 않는 O(n)보다도 빠른 속도를 가집니다.
하지만 우리 변태같은 개발자들... O(log n)의 시간 복잡도는 성에 차지 않았는지 더 효율적인 자료구조를 만들기 시작합니다. 그것이 바로 레드-블랙 트리입니다.
레드 블랙 트리에 대해 잠깐 알아보도록 하죠
레드 블랙 트리
레드 블랙 트리는 이진 탐색 트리의 변형된 모델로 앞서 말했듯이 탐색시간을 2배가까이 줄여주는 자료구조입니다.
레드 블랙 트리는 이진 탐색 트리에서 조건이 몇개 더 추가됩니다.
- Root Property : 루트 노드의 색깔은 검정이다.
- External Property : 모든 external node 들은 검정이다.
- Internal Property : 빨강 노드의 자식은 검정이다. == No Double Red(빨간색 노드가 연속으로 나올 수 없다.)
- Depth Property : 모든 리프노드에서 Black Depth는 같다. == 리프노드에서 루트노드까지 가는 경로에서 만나는 블랙 노드의 개수는 같다.
이런 조건에 의해 이진 탐색 트리를 색칠해나가면 됩니다.
간단하게 예제를 통해 알아볼까요?
루트 노드의 색깔은 검정을 줬습니다.

이제 값들을 삽입해보겠습니다.
참고로, 삽입되는 노드의 색은 무조건 빨간색 입니다.
아니 그럼 세번째 삽입되는 노드도 빨간색이면 3번 조건에 위배될 가능성이 있겠네요?
그것에 대한 해결책이 뒤에 나옵니다. 우선 무작정 넣어보도록 하죠

2와 8을 넣어봤습니다. 2는 4보다 작으니까 왼쪽 8은 4보다 크니까 오른쪽. 잘 들어갔습니다. 값을 하나 더 넣어보겠습니다.

3은 4보다 작고 2보다는 크니 해당 위치로 이동하겠죠?
하지만, 이렇게 되는 순간 3번 조건을 위반하게 됩니다. Red의 자식은 Black이어야 하는데 Red가 왔네요.
이러한 상황을 Double Red 라고 하며 레드 블랙 트리에서는 이러한 Double Red를 해결하기 위한 두가지 방법을 제시합니다.
바로 Restructuring과 Recoloring이죠

우선 그림으로 정리해봤는데요.
Double Red를 해결하는 방법은 현재 삽입된 노드의 uncle node의 색깔에 따라 수행하는 프로시저가 다릅니다.
말 그대로 삼촌 노드 즉, 부모의 형제 노드 여기서는 w가 되겠네요
w가 검정일땐 Restructuring
w가 빨강일 땐 Recoloring을 진행합니다.
Restructuring을 먼저 알아보겠습니다.
Restructuring
Restructuring은 현재 삽입된 노드와 내 부모노드와 내 부모의 부모를 가지고 Restructuring을 진행합니다.
Restructuring은 다음과 같은 순서로 진행됩니다.
- 삽입된 노드를 '나'라고 하면 나와 내 부모, 내 부모의 부모를 오름차순으로 정렬
- 무조건 가운데 있는 값을 부모로 만들고 나머지 둘을 자식으로 만든다.
- 올라간 가운데 있는 값을 검정으로 만들고 두 자식을 빨강으로 만든다.
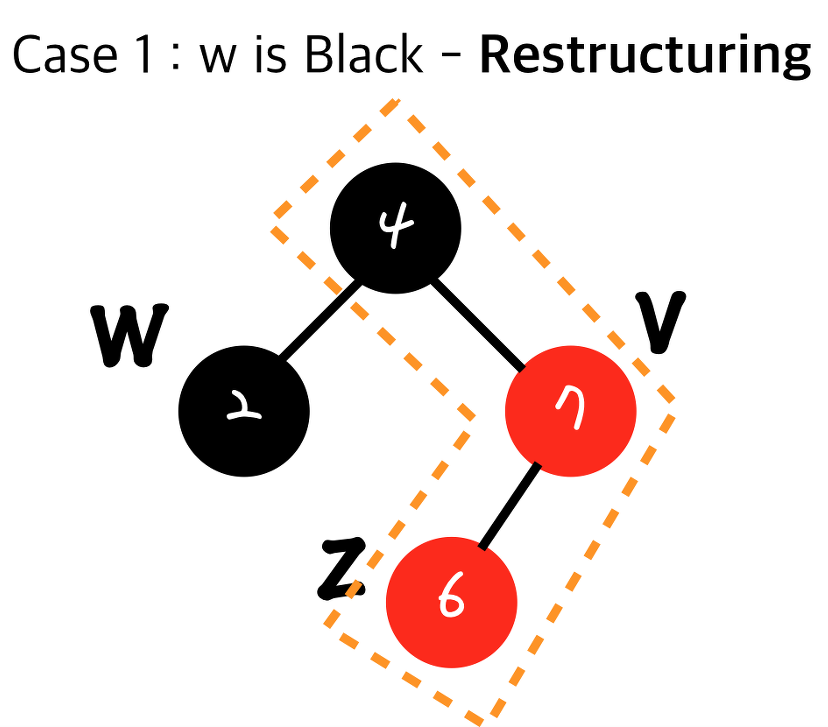
현재 삽입된 노드와 부모노드 부모의 부모노드를 잡았습니다. 그리고 이제 순서대로 하면 됩니다.
1번 오름차순이었죠?

오름차순으로 정렬이니 이런 식으로 되겠네요. 이제 가운데 있는 값을 부모로 만들고 나머지 둘을 자식으로 만듭니다.
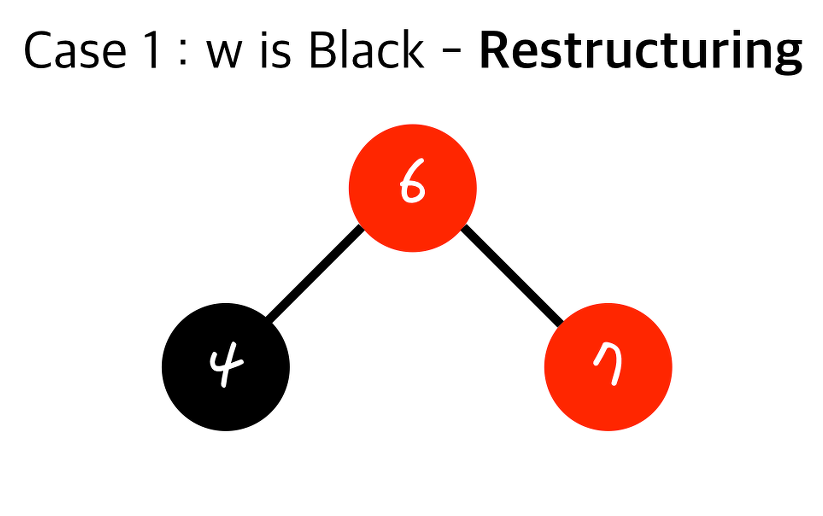
6보다 작은 4를 왼쪽에 두고 6보다 큰 7을 오른쪽으로 두는 것은 이진 탐색 트리이니 당연하겠죠?
마지막 단계로 부모로 올라간 6을 검정으로 그 자식들을 빨강으로 만듭니다.

바로 이렇게요. 그리고 이제 원래 4의 자식이었던 2를 추가하면 됩니다.
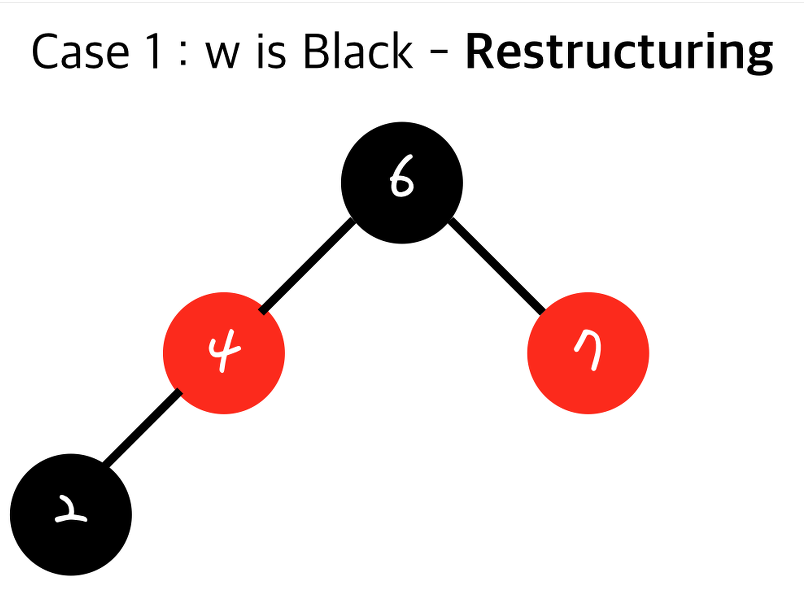
자 이제 Restructuring이 끝났습니다. 정말 Double Red가 없어졌죠?
Restructuring은 다른 서브트리에 영향을 끼치지 않기 때문에 한번의 Restructuring이면 끝납니다. 여기서 말하는 영향이란 Black Depth에요. 위에서 4번 조건 기억나시죠?
모든 리프노드에서 Black Depth는 같다인데 Double Red를 해결하기 전과 해결한 후의 Black 노드의 개수에 변화가 없기 때문에 다른 서브트리에 영향을 끼치지 않게 됩니다.
또한, Restructuring 자체의 시간 복잡도는 O(1)에서 끝나지만 Restructuring은 어떤 노드를 삽입해야만 일어나기 때문에 결과적으로 총 수행시간은 O(log n)입인다. 현재 노드가 들어갈 위치를 먼저 찾아야 하기 때문이죠.
자 이제 Restructuring은 끝났습니다. 그럼 다음엔 Recoloring을 알아볼까요?
Recoloring
Recoloring의 과정은 다음과 같습니다.
- 현재 삽입된 노드의 부모와 그 형제를 검정으로 만들고 부모의 부모를 빨강으로 한다.
- 부모의 부모가 루트노드가 아니었을 시 Double Red가 발생할 수 있다.
이번에도 예제를 통해 알아보도록 하죠
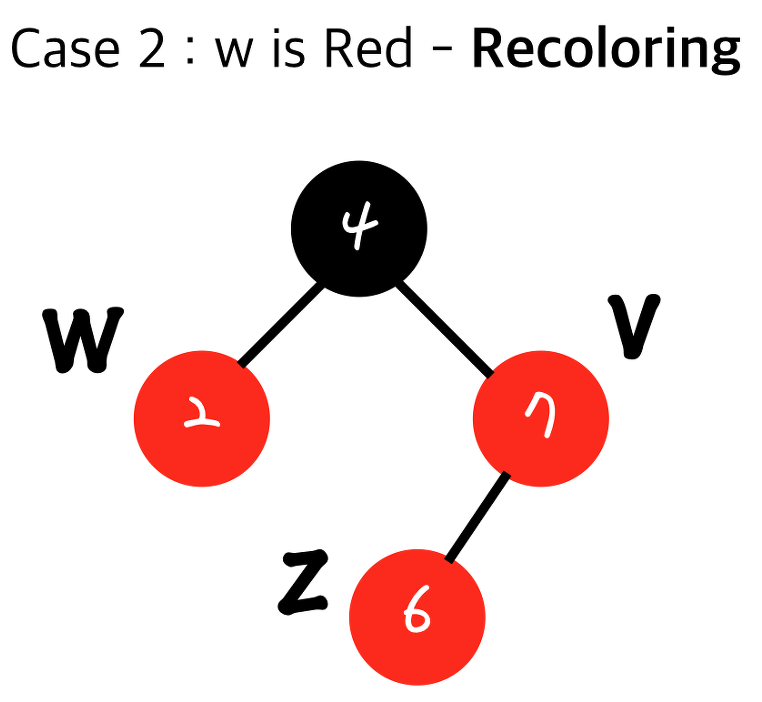
현재 삽입된 노드의 부모(v)와 그 형제(w)의 색깔을 검정으로 만들어줍니다.
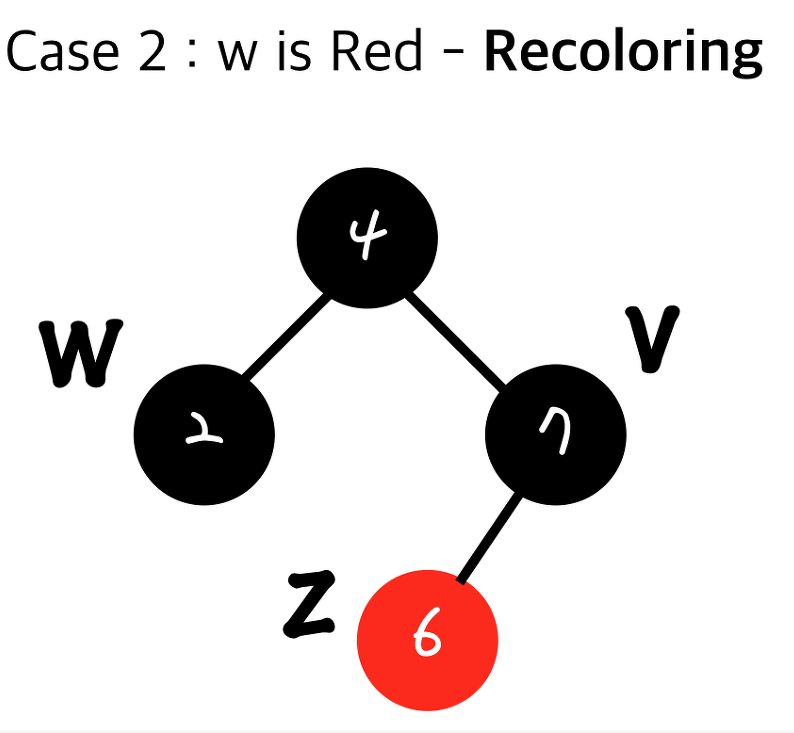
그리고 부모의 부모 노드를 빨강으로 만들어줍니다.

하지만 만약 부모의 부모가 루트 노드였다면, 레드 블랙 트리의 1번 조건에 의해 검정으로 바뀌게 됩니다.

어? 이거 맞게 된건가요? 검빨검빨 이런식으로 번갈아가면서 나와야 되는거 아닌가요? 라고 의심이 들 수 있습니다.
하지만 위와 같은 상황은 레드 블랙 트리의 네가지 조건에 전부 부합합니다. 따라서 위의 상황은 올바른 상황입니다.
하지만 이런 경우는 그렇다 치더라도 만약 우리가 Recoloring 한 트리가 엄청 큰 트리의 서브트리였다면 어떨까요?

그럼 이 상황일텐데 이 위에 부모 노드가 빨강이면 어떡하죠? 어떡하긴요... 또 Recoloring을 하던가 Restructuring을 진행합니다.
계속 Recoloring을 진행하다가 삼촌 노드의 색이 검정이면 Restructuring을 진행하고 Restructuring은 다른 서브트리에 영향을 끼치지 않으므로 여기서 종료가 됩니다.
이렇게 레드 블랙 트리에 대해서 알아봤습니다. 이렇게 네가지 조건에 만족하게 이진 탐색 트리를 구성하게 되면 이진 탐색 트리임에도 불구하고 높이가 log n에 바운드 됩니다.
자 여기까지 Tree 자료구조 그리고 탐색에 가장 많이 사용되는 이진 트리, 이진 탐색 트리에 대해서 알아봤습니다. 이번엔 좀 복잡한 내용들이 많아서 이해하기위해 긴 시간을 들였습니다. 여러분은 어떠셨나요?
긴 글 읽어주셔서 감사합니다. 다음에도 더 좋은 포스팅으로 찾아뵙도록 하겠습니다.
출처
https://velog.io/@kimdukbae/%EC%9E%90%EB%A3%8C%EA%B5%AC%EC%A1%B0-%ED%8A%B8%EB%A6%AC-Tree
[자료구조] 트리 (Tree)
사진의 출처 : 링크트리(Tree)는 그래프의 일종으로 정점과 간선을 이용하여 데이터의 배치 형태를 추상화한 자료구조이다.서로 다른 두 노드를 연결하는 길이 하나뿐인 그래프를 트리라고 부른
velog.io
https://jud00.tistory.com/entry/%EC%9E%90%EB%A3%8C%EA%B5%AC%EC%A1%B0-%ED%8A%B8%EB%A6%ACTree%EB%9E%80
[자료구조] 트리(Tree)란
이번에는 자료구조 중 하나인 트리(Tree)에 대해서 정리하겠습니다. 가급적이면 쉽고 간단하게 설명할 예정이며, 더 깊고 많은 내용을 알고 싶으시다면 다른 블로그를 참고하시기 바랍니다 :) 트
jud00.tistory.com
https://zeddios.tistory.com/237
알고리즘 ) Red-Black Tree
안녕하세요 :) Zedd입니다. 오늘은 알고리즘 파티인가요?이 전글 와 Red-Black Tree가 같은 강의자료에 있길래..얼른 iOS글도 써야하는데...ㅎ_ㅎ 뭐 연휴는 기니까....히유ㅠㅠ강의자료 보다보니까, 이
zeddios.tistory.com
'CS 지식 > 자료구조, 알고리즘' 카테고리의 다른 글
| 자료구조 : Stack (0) | 2023.02.25 |
|---|---|
| 자료구조 : Set (0) | 2023.02.23 |
| 자료구조 : Hash (0) | 2023.02.23 |
| 자료구조 : Map (0) | 2023.02.18 |
| Two-Pointers-Algorithm (0) | 2023.02.15 |