Two-Pointers-Algorithm
two pointers algorithm (이하 투 포인터 알고리즘) 알고리즘은 말 그대로 포인터를 사용해 배열에 쉽게 접근할 수 있게 해줍니다.
자바에서도 배열에 쉽게 접근하기 위해 포인터를 사용하는 경우가 종종 있습니다.
보통 lt (left), rt (right) 혹은 s (start), e (end) 혹은 p1, p2 이런식으로 포인터를 정해서 값을 하나씩 증가시키면서 배열을 참조합니다.
투 포인터 알고리즘을 사용하는 문제는 비교적 자주 만나볼 수 있으며 한번 익혀두면 나중에 써먹기 정말 편하다고 합니다. 물론 저는 세번밖에 안써봤습니다.
먼저 문제를 확인해보시죠

문제를 해석하자면 N개로 된 수열에서 N개의 부분집합 중에서 M이 되는 개수가 몇개냐라고 물어보는 문제입니다.
이 문제를 모든 경우의 수를 확인하기 위해 2중 for 문을 이용해 풀기 시작하면 시간 복잡도가 O(n^2)이 걸리게 되어 시간초과로 오답이 나오는 경우입니다.
이 문제 풀이의 핵심은 왼쪽에 존재하는 s (start) 그리고 오른쪽에 존재하는 e (end) 를 이용해 인덱스를 하나씩 이동시키면서 확인하는 방식입니다.
즉, 맨 처음에는 s 와 e 가 0이며 항상 s <= e 를 만족해야 합니다. 2개의 포인터는 현재 부분 배열의 시작과 끝을 가리키는 역할을 합니다.
이것을 해결하기 위한 알고리즘은 아주 간단합니다.
- 만약 현재 부분합이 M 이상이거나 이미 e = N (e 가 끝에 닿으면) s를 하나 증가시킵니다.
- 그렇지 않다면 e 를 하나 증가시킵니다.
- 현재 부분합이 M과 같으면 결괏값을 하나 증가시킵니다. 그러면서 s 를 하나 증가시킵니다.
- s = e 인경우에는 sum (M) = 0 이라 정의합니다. 이 경우에는 e 를 하나 증가시킵니다.
이제 그림과 함께 풀이해보도록 하겠습니다.

현재 상태는 초기상태입니다. s 와 e 가 인덱스 0에 위치하고 있습니다.

s 와 e 가 같기때문에 e 를 하나 증가시켰습니다. 이렇게 되니 부분합이 1이 됐네요. 부분합이 목표값인 M보다 작기 때문에 e 를 하나 더 증가시킵니다.
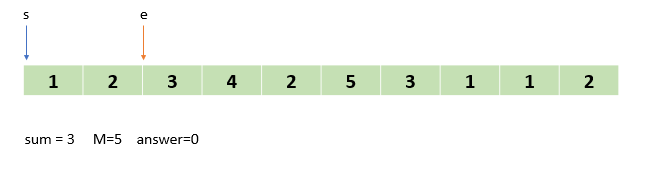
e 를 하나 증가시켰더니 부분합이 3이 되었습니다. 여전히 M 보다 작기 때문에 오른쪽으로 한 칸 더 이동합니다.

e 가 2를 가리키고 s는 0을 가리키고 있는 상태입니다. 부분합은 6이네요 우리가 원하는 숫자인 5보다 크기때문에 s를 한칸 앞으로 이동시킵니다.

s 가 한칸 이동해서 인덱스 1을 가리키게 되었습니다. 이제 부분합이 5가 되었습니다. 그러니 3번 알고리즘에 의해 결괏값을 하나 증가시키고 s 를 한칸 앞으로 이동시키겠습니다.
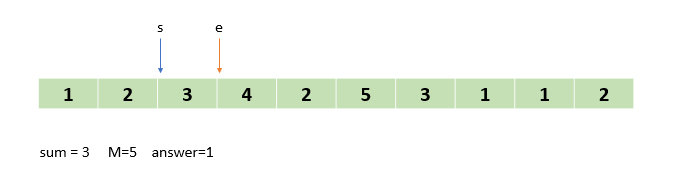
어떤 느낌인지 이제 슬슬 아시겠죠?
이 알고리즘을 다 따라가다보면 결국 e 는 종점에 도착하게 됩니다.

이제 남은건 s 가 e 와 같아질 때까지 앞으로 증가시키면 됩니다.

이렇게 s 가 배열의 끝에 다다르면 반복문을 종료합니다. 이렇게 answer = 3 을 찾아내는 과정이 끝났습니다.
이처럼 투 포인터 알고리즘을 사용하면 O(n) 의 시간복잡도로 문제를 해결할 수 있습니다. 어떻게 O(n) 일까요? s 와 e 는 매 과정에서 무조건 1씩 증가하게 됩니다. s 와 e 는 최대 N 까지 증가할 수 있으며 s <= e 이기 때문에 둘이 증가하는 과정은 최대 N 번만 반복될 것입니다.
더 자세히 말하면 O(2n)이지만 우리는 앞서 시간복잡도에서 n이 무한대로 가면 의미가 퇴색되기 때문에 가장 기본이되는 표기법을 사용합니다.
따라서 투 포인터 알고리즘을 사용하게 되면 O(n^2)가 걸리는 문제를 O(n)에 해결할 수 있습니다.
하지만 투 포인터 알고리즘이 모든 정답을 찾아내는가에 대한 의문을 가질 수 있습니다. 이것에 대해서는 아래와 같이 증명할 수 있습니다.

S 부터 E 까지의 구간합이 M인 구간이 있습니다. 우리는 이 구간이 몇 개 있는지 찾아야합니다. 이때 투 포인터 알고리즘을 사용하면 저 구간을 놓칠 수 없습니다. 만약 저 구간을 놓치는 경우를 가정해볼까요?
1. s = S 가 되기 전에 e 가 E 를 넘어가는 경우
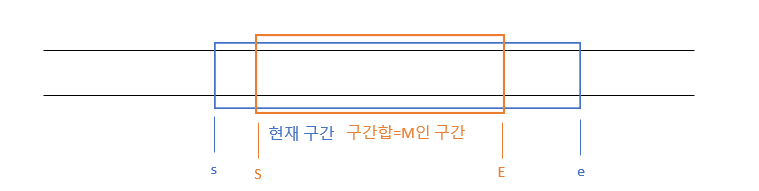
위와 같은 상황은 벌어지지 않습니다.

s 와 e 는 한 칸씩 오른쪽으로 이동합니다. 이때 e 는 무조건 E 를 한 번은 지나가게 되는데, 만약 s 가 S 보다 왼쪽에 있다면, s 부터 e 까지의 구간합은 무조건 M 보다 클 수밖에 없습니다. 물론 이것은 배열이 모두 자연수라는 가정에서입니다. 배열에 음수가 있다면 성립하지 않습니다. 하지만 위의 경우에서는 e 가 E 보다 더 오른쪽으로 이동하는 일은 벌어지지 않습니다.
2. e 가 E 가 되기전에 s 가 S 를 넘어가는 경우
이 경우도 1번과 같은 방식으로 증명할 수 있기 때문에 넘어가도록 하겠습니다.
결론
투 포인터 알고리즘은 모든 경우에수를 고려한다.
여기까지 투 포인터 알고리즘에 대해서 알아봤습니다. 알고리즘은 재밌는듯 하면서도 어려워서 쉽지않네요. 제가 모르는게 많아서 앞으로 더 재밌는 알고리즘이 나올듯 하네요.
긴 글 읽어주셔서 감사합니다. 오늘도 즐거운 하루 보내세요~
출처
GitHub - WooVictory/Ready-For-Tech-Interview: 💻 신입 개발자로서 준비를 하기 위해 지식을 정리하는 공간
💻 신입 개발자로서 준비를 하기 위해 지식을 정리하는 공간 👨💻. Contribute to WooVictory/Ready-For-Tech-Interview development by creating an account on GitHub.
github.com
https://code-lab1.tistory.com/276
[알고리즘] 투 포인터 알고리즘(Two-Pointers Algorithm)이란? 백준 2003번 C++ 풀이
투 포인터 알고리즘(Two-Pointers Algorithm)이란? 투 포인터 알고리즘은 말 그대로 두 개의 포인터를 이용해 문제를 해결하는 알고리즘을 뜻한다. 보통 l(left), r(right)나 s(start), e(end) 같은 식으로 포인
code-lab1.tistory.com
'CS 지식 > 자료구조, 알고리즘' 카테고리의 다른 글
| 자료구조 : Tree (0) | 2023.02.23 |
|---|---|
| 자료구조 : Hash (0) | 2023.02.23 |
| 자료구조 : Map (0) | 2023.02.18 |
| 에라토스테네스의 체 (소수 구하기) (0) | 2023.02.14 |
| 시간복잡도 (0) | 2023.02.14 |