안녕하세요. 요즘 AI 엔지니어링 업무를 하면서 관련된 것들을 공부를 하니 더 재밌는 것 같네요. 이번 포스팅에선 Transformer 알고리즘이 담긴 논문이 출판됐을 당시부터 있었던 근본 개념들을 알아보면서 그때의 한계를 현재는 어떻게 극복했는지를 중점으로 정리할 예정입니다.
LLM을 논하기 이전에 가장 중요한 개념이 바로 Transformer이고 개발자가 아닌 분들도 AI에 조금만 관심이 있다면 한 번쯤 들어봤을 내용인데요. 저는 이론 없는 실전은 기반 없이 무작정 높게만 쌓은 건축물이라는 철학이 강해서 현재 실전에서 충분히 써먹지 못하더라도 알고 안쓰는거랑 모르고 안쓰는거랑은 차이가 있다고 생각하는 주의입니다.
AI 엔지니어링이라는 분야가 실제 그래픽카드 서버가 없으면 제약사항도 많아서 실전을 많이 경험해볼 수 없기도하거니와 그렇기에 이론이 더더욱 중요한 것 같습니다.
서론이 길었습니다. Transformer 알고리즘에 대해서 바로 들어가보죠!
들어가기 전에..
우선 자세한 내용을 들어가기 전에 이번 포스팅은 다음과 같은 순서를 따릅니다.
- Attention 연산이란?
유사도 계산 : 쿼리와 키의 관계에 초점을 맞춰서 서술할 예정입니다.
스케일링 : 모델의 파라미터가 너무 커짐에 따라 보정 작업이 들어가는 과정에 대해 이야기합니다.
Softmax : 모델이 행렬 계산의 결과를 0~1 사이의 확률로 볼 수 있도록 하는 과정에 대해 이야기합니다.
가중합 : 가중치와 실제 값을 매칭하여 벡터에 문맥을 부여하는 과정을 이야기합니다. - 연산 부하를 줄여라! Flash Attention
Attention 연산의 가장 큰 문제는 행렬 값을 계산하기 위한 연산량이 어마어마하다는 것인데요. 현재 모델들은 이 연산을 줄이기위한 공학적인 트릭을 썼는데 이 내용을 다룬 Flash Attention에 대해서 잠깐 짚고 넘어갈 예정입니다. - Positional Encoding
벡터가 널린 사막에서 맥락이라는 방향을 유지하기 위해 어떤 방법론을 사용하는지 Transformer 논문이 등장했을 때랑 현재는 어떻게 바뀌었는지, 그 때 당시의 한계점을 어떻게 기술적으로 해결했는지에 대해서 서술합니다. - Encoder와 Decoder
Transformer 초기엔 맥락을 파악하는 Encoder와 텍스트 생성을 담당하는 Decoder가 존재했는데요, 요즘 모델들을 보면 Decoder-Only 라는 표현을 자주 볼 수 있게 되는데 Encoder가 없으면 어떤 문제가 생기고 이 문제를 어떻게 해결했는지에 대해서 서술합니다.
여기서 중점적으로 볼 부분은 바로 유사도 계산과 스케일링인데요. Softmax와 가중합은 깊이 들어가니까 수학공식이 난무해서 도저히 포스팅에 쓸 수 없었습니다.
그래서 이번엔 다른 포스팅과 다르게 조금 가볍게 갈 예정입니다.
이제 본격적으로 들어가보시죠!
Attention 연산이란?
Attention 연산은 Transformer가 탄생한 최초의 논문에서도 언급되었을만큼 굉장히 근본중에 근본이고 아직도 많은 모델들이 이 연산을 기반으로 텍스트를 생성하고 있는데요.
Attention 연산은 다음과 같은 수식을 가지고 있습니다.
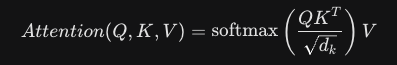
수학적인 얘기는 안하고 공학적으로 해석한 내용이 주를 이루기 때문에 걱정하지 않으셔도 됩니다. (저도 수학 겁나 못해요)
먼저, 쿼리와 키를 내적하는 "유사도 계산"파트와 벡터의 차원이 커지면 Softmax 연산에 노이즈가 생길 수 있어 이 부분을 억제하는 "스케일링" 구간이 있습니다. 그리고 이를 모델이 잘 알아먹을 수 있게 확률로 표현하는 "Softmax"단계가 있고 마지막으로 맥락과 값을 행렬곱한 "가중합" 단계가 있습니다.
이제 천천히 하나씩 살펴보도록 하죠.
유사도 계산
먼저 첫 번째 단계는 쿼리와 키를 내적하여 유사도를 구하는 단계입니다. 쿼리와 키를 내적하는 것이 어떻게 유사도로 이어질 수 있는가를 먼저 보면 답은 두 위치 벡터의 각도가 핵심입니다.
내적은 두 벡터의 크기와 그 사이의 코사인 값을 곱하면서 이루어지는데 코사인 함수의 특징상 사잇각이 0도가 되면 코사인 값은 최대가 되어 내적값이 최대가 되고, 90도가 되면 코사인 값이 0이 되어 내적 값이 0으로 떨어집니다.
따라서, 두 벡터의 내적값으로 얼마나 이 두 벡터가 문맥상 유사한지 판단할 수 있는 척도가 됩니다.
Attention 연산에는 쿼리 (Q), 키 (K), 값 (V) 이렇게 세개로 이루어져있는데 각각의 의미는 다음과 같습니다.
- Query : "나는 이런 정보를 찾고있어!" 라는 요구사항입니다.
- Key : "나는 이런 특징을 가진 정보야" 라는 인덱스와 같습니다.
- Value : "나는 실제로 이런 값이야" 라는 값 그자체입니다.
그런데 유사도 얘기를 하는데 어째서 쿼리와 키를 내적하는걸까요? 이 둘이 무슨 공학적인 의미가 있길래 다른 값도 아닌 쿼리와 키를 내적하는걸까요?
쿼리와 키를 내적한다는 의미는 내가 던지는 질문과 내가 실제로 찾는 대상간의 연관관계를 내적 값의 크기로 판단하는 것입니다.
- Query : "제가 찾고 있는건 빨갛고 동그란 과일입니다."
- Key : "저는 사과를 가리키고 있습니다." / "저는 바나나를 가리키고 있습니다." / "저는 수박을 가리키고 있습니다."
- Value : "사과" / "바나나" / "수박"
그럼 쿼리와 키를 내적하면 다음과 같은 연관성을 얻을 수 있습니다.
- 빨갛고 동그란 과일과 사과와의 관계
- 빨갛고 동그란 과일과 바나나와의 관계
- 빨갛고 동그란 과일과 수박과의 관계
즉, 내가 던지는 질문과 내가 찾는 값 사이에서의 연관성을 찾기 위해 쿼리와 키를 내적하는 것이죠.
스케일링
벡터의 차원 수가 커지면 (모델의 파라미터가 커지면) 내적 값의 절댓값도 확률적으로 커지게 되는데요. 이때 내적 값이 너무 커지면 후술할 Softmax 함수에서 문제가 생깁니다. Softmax는 입력값이 커지면 결괏값도 커지고, 입력값이 작으면 결괏값도 작아진다는 특징이 있어서 벡터가 커지면 이 결괏값이 너무 크거나 너무 작은 극단적인 형태를 띄게 됩니다.
이게 커지면 뭐가 문제길래 그런걸까요?
이렇게 값이 극단적으로 몰리면 Gradient (기울기) 가 0에 수렴하는 문제가 발생합니다.
기울기가 0이 된다는 의미는 수학적으로 미분값이 0이 된다는 의미이고 모델을 학습시킬 때 역전파를 사용하고 이때 손실 함수(L)를 가중치(W)로 미분한 값을 이용해서 점수를 메기기 때문에 문제가 됩니다.
LLM 모델을 학습시킬 때 주요하게 사용되는 개념인 역전파는 딥러닝에서 파생된 개념인데 추후에 이 개념에 대해서도 포스팅할 예정입니다. 우선은 모델을 학습시킬 때 사용하는 방법론이라고만 이해하고 넘어가도 될 것 같습니다.
여기서 손실 함수와 보상 함수에 대한 개념이 등장하는데 이건 짚고 넘어가도록 하죠.
- 손실 함수 : 손실 함수는 연관 없는 것들에 감점을 하는 방식입니다. 점수를 더하지는 않고 무조건 감점하기만 하기 때문에 이 값을 바탕으로 점수가 높은 것들은 연관성이 높다고 판단하고 점수가 낮은 것들은 연관성이 낮다고 판단하게 되는것이죠.
- 보상 함수 : 보상 함수는 연관 있는 것들에 가점을 하는 방식입니다. 점수를 깎진 않고 무조건 가점하기만 하기 때문에 모델이 어떤 방향으로 가야하는지 방향성을 제시해줍니다. (이 방향으로 가면 점수를 더 많이주네? 앞으로 여기로 가야겠다.)
손실 함수는 주로 딥러닝에서 사용되는 개념이고, 보상 함수는 주로 강화 학습에서 사용되는 개념이기 때문에 살짝 다르지만 그래도 점수를 깎거나 더함으로써 모델이 어떤 방향으로는 가지 말아야할지, 어떤 방향으로는 가야할지를 알려주는 개념이라고 이해하시면 될 것 같습니다.
손실 함수에 가중치를 미분할 때 만약에 이 값이 0에 가까워지면 Softmax를 통과할 때 작은 값이 더 한없이 작아지는 효과가 생겨 기울기가 0이 되어버리면 모델은 "수정할 방향을 잃어버렸다" 라고 판단하고 모델은 더이상 똑똑해지지 않고 그 상태로 멈춰버리게 됩니다. 이를 Dead Neuron 즉, 죽어버린 뉴런이라고 부릅니다.
이 때문에, 내적 값의 분산을 일정하게 유지하여 Softmax가 안정적인 기울기를 갖도록 표준화하는 작업이 바로 스케일링 작업이라고 볼 수 있습니다.
Softmax
Softmax는 쉽게 얘기해서 유사도를 확률로 나타낸 것입니다.
유사도는 쿼리와 키의 내적이라고 했는데, 내적을 하면 결괏값이 벡터의 형태로 존재하게 됩니다. (내적의 결괏값이 벡터가 아닌 스칼라인 것과는 조금 이야기가 다릅니다) 여러 차원에 흩뿌려져 있는 데이터들을 LLM모델이 이해하기 힘들기 때문에 이를 0과 1사이의 확률로 나타내는 것이죠.
이때 Softmax는 내부적으로 자연상수 e의 거듭제곱 꼴로 사용되는데 이는 큰 값은 더 크게, 작은 값은 더 작게 만드는 효과가 있습니다. 그 결과 시퀀스 내의 여러 단어 중 현재 쿼리의 정말 관련이 있는 단어에게만 점수를 몰빵해주고 관련 없는 단어는 0에 가깝게 죽어버리는 효과가 생깁니다.
가중합
이전 단계에서는 어떤 단어에 얼마나 집중할지 확률을 구한 것이라면 이제 이 확률을 실제 값인 V와 결합하여 실제 정보를 그 확률만큼 가져와야합니다.
각 단어의 Value 벡터에 Softmax로 구한 가중치를 행렬곱하여 모두 더한 뒤, 만약 "사과"라는 단어의 쿼리가 "맛"이라는 키와 0.9만큼 연관되어 있다면, "사과"의 최종 출력 벡터에는 "맛"이라는 단어가 가진 Value 정보가 90퍼센트 섞이게 됩니다.
최종적으로 이 가중합을 통해 나온 벡터는 단순한 단어 벡터가 아니라 주변 문맥 정보가 연관성만큼 가중치가 섞인 "문맥이 반영된 벡터"가 됩니다.
Flash Attention
Attention의 가장 큰 문제는 "모든 단어가 모든 단어를 바라본다"라는 것입니다.
예를 들어서 문장의 길이가 N이라면 쿼리와 키를 행렬곱하는 순간 N x N의 Attention Map이 형성됩니다. 문장이 만약 천개의 단어로 이루어져있다면 1,000 x 1,000 으로 100만번, 문장의 단어가 만개라면 1억번, 뭐 이런식인거죠.
단순히 연산 횟수도 병목의 문제지만 더 끔찍한건 메모리의 병목입니다. 이 거대한 행렬을 GPU의 메모리에서 썼다 읽었다 하는 과정에서 어마어마한 병목이 생깁니다. 이 병목을 "폰 노이만 병목"이라고도 부르죠.
이때 등장하는 개념이 바로 Flash Attention입니다.
Flash Attention은 알고리즘 자체를 바꾼 것이 아니라 컴퓨팅 아키텍처 최적화로 이 문제를 해결했습니다. N x N 행렬을 한번에 처리하지 않고 GPU의 아주 작지만 빠른 내부 캐시 메모리인 SRAM 안에서 계산을 끝내고 최종 결과만 밖으로 내보내는 방법을 택했습니다.
느려터진 메모리에서 행렬 값을 계산하는 것보다 SRAM에서 필요한 것만 계속 받아다가 계산하는 것이 더 빠르기 때문에 이 방법이 채택되었다고 볼 수 있습니다.
Positional Encoding
Attention 연산이 병렬 처리에 유리했던 이유는 "순서와 상관없이 한번에 계산하기" 때문이었는데요, 그렇지만 언어는 역설적이게도 순서가 가장 중요합니다.
"개가 사람을 물었다"와 "사람이 개를 물었다"는 의미적인 차이가 하늘과 땅차이이기 때문입니다.
이 문제를 해결하기 위해 각 단어의 "임베딩 벡터"에 해당 단어의 "위치 정보 벡터"를 더해주는 방법으로 이 문제를 해결했습니다.
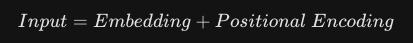
이 작업은 Attention 연산을 시작하는 맨 앞단에서 적용되는데 이 때 흐름은 다음과 같습니다.
- Tokenization : 문장을 토큰 ID로 쪼갭니다. ["안녕", "하세", "요"] -> [101, 2045, 312] 이렇게 말이죠.
- Embedding Lookup : 각 정수 ID를 거대한 테이블인 임베딩 층에서 찾아 의미를 가진 고밀도 벡터로 바꿉니다.
[v_안녕, v_하세, v_요] 이렇게 말이죠. - Positional Encoding : 이때 각 위치에 맞는 위치 벡터를 생성해서 더해줍니다. [v_안녕+P_1, v_하세+P_2, v_요+P_3]
- 이제 순서 정보가 포함된 이 벡터들이 Attention 레이어로 진입합니다.
이 위치정보를 더해주는건 알겠는데 이 위치정보를 어디서 가져와서 더해주는걸까요?
이 위치 정보 벡터는 고전적으로 sin, cos 함수를 이용했습니다. Transformer가 탄생하게 된 최초의 논문에서는 서로 다른 주기를 가진 사인 함수와 코사인 함수를 사용했는데, 각 위치마다 서로 다른 주파수의 삼각함수 값을 조정해 모든 위치가 서로 다른 고유한 벡터를 갖게 했습니다.
삼각함수의 덧셈정리 덕분에 모델은 현재 단어로부터 k만큼 떨어진 단어와의 상대적인 거리를 선형 변환으로 쉽게 알 수 있었죠.
이렇게했더니 문제가 생겼습니다.
모델을 2k 토큰으로 학습했는데 사용자가 입력을 20k짜리 코드를 들고오면 어떻게 될까요?
모델 입장에서는 "나는 2k까지밖에 모르는데 그 다음은 어떻게 해결해야하지?" 이런 문제가 생겼습니다. 이렇게 되면 할루시네이션이 폭발해서 모델이 이상한 답변을 하게 되는 문제가 있었고 이를 해결해야했습니다.
그래서 요즘은 RoPE라는 방법을 사용합니다.
RoPE
예를 들어서 1번 단어, 2번 단어, 3번 단어가 있다고 가정해봅시다. 이때 고정된 각도를 먼저 세팅해줍니다. 임의로요. 이때 각을 세타라고 합시다.
그럼 1번 단어는 1세타, 2번 단어는 2세타, 3번 단어는 3세타, n번 단어는 n세타 이런식으로 표현할 수 있습니다. 그럼 1번 단어와 n번 단어의 상대적인 위치는 n-1세타가 됩니다.
이게 무슨 의미를 가지냐하면 보통 모델을 학습시킬 때는 파라미터가 어마어마하게 큰 모델을 학습시키는데 이를 큰 토큰으로 학습시킬 수는 없습니다. 그래서 보통 2k정도 되는 토큰을 학습시키는데 앞서 언급했듯이 만약 사용자가 30k짜리 토큰을 들고오면 모델 입장에서는 난처해집니다.
하지만 이때 RoPE를 사용하면 2k이후에도 2001은 2001세타 2002는 2002세타 이런식으로 2k이후의 토큰도 상대적인 위치를 알 수 있게 되는겁니다.
그래서 요즘 LLM들은 어마어마하게 많은 양의 Input 토큰을 입력할 수 있는 것입니다.
그런데 이건 뭔가 이상합니다. 만약 sLLM같은 모델로 개발해보면 입력 토큰이 제한되어 있는 경우가 대부분입니다. 이건 어떻게 된걸까요?
보통 이런 sLLM모델도 같은 방법론이 적용되어 있습니다. 하지만 이는 백엔드에서 Connection Pool이나 JMV Heap Memory를 제한하는 것과 같은 이치입니다. 하드웨어가 수용할 수 있는 토큰과 모델이 이해하는 토큰은 다르기 때문입니다.
아무리 Flash Attention을 써도, 문장이 길어지면 KV Cache가 차지하는 메모리가 선형적으로 늘어나고 작은 sLLM모델이 감당 가능한 메모리 영역을 넘어서면 OOM이 발생하기도 합니다. 또한, 모델 자신이 학습한 토큰 이후의 범주까지 이해가 가능하다고 해도 이를 정확히 추론하는 능력은 별개의 문제입니다.
학습할 때 주로 8k 위주로 학습했다면 32k가 들어올 때 이해는 하지만 정확도가 떨어지는 현상이 발생합니다. 그리고 sLLM 뿐만 아니라 모든 LLM이 가진 고질적인 문제가 바로 앞부분과 뒷부분은 잘 기억하는데 중간 내용을 까먹는 현상이 있습니다. 때문에, 제조사에서는 이 품질이 일정 수준 유지되는 지점을 제한사항으로 공표하는 것입니다.
Encoder와 Decoder 그리고 Decoder-Only
원래 오리지널 Transformer에서는 Encoder와 Decoder가 둘 다 있었습니다. Encoder는 문장 전체를 한꺼번에 보고 각 단어의 의미를 추출하는데 특화되어있고 Decoder는 Encoder가 준 정보를 바탕으로 한 글자씩 결과를 생성하는데 특화되어있습니다.
그런데 연구를 하다보니 굳이 Encoder가 필요한가 의문이 들었고 Decoder만 가지고도 앞에 나온 단어들을 토대로 다음 단어를 맞히는 학습을 시키면 충분히 똑똑해지는 것을 확인했습니다. 그래서 Encoder를 뜯어내고 생성에 최적화된 Decoder만 남게 된 것입니다.
Decoder-Only 모델의 가장 큰 특징은 "미래를 볼 수 없다"라는 점입니다. Encoder로 미래를 볼 수 있게 된다면 학습이 안되기 때문인데 정답지를 보고 정답을 맞추라고 하는 것과 같은 이치이기 때문입니다. 이 때문에 Decoder-Only 모델은 자기가 뱉은 말을 다시 입력으로 넣는 무한루프 구조가 되었습니다.
만약 입력으로 "오늘 점심은" 이라는 단어를 생성해냈고 출력으로 "돈까스"라는 단어를 생성했다면 다음 단어를 생성할 때는 입력으로 "오늘 점심은 돈까스"라고 넣고 출력을 하게 됩니다. 그럼 "오늘 점심은 돈까스 먹자" 이렇게 문장이 완성되는 것입니다.
Decoder-Only 모델은 구조가 단순해서 파라미터를 수조개로 늘려도 병렬 처리가 쉬웠고 학습 효율이 좋았습니다. 또한, 다음 단어 맞히기라는 단순한 원리 하나로 코딩, 수학, 번역, 대화 등 모든 언어를 사용하는 일을 잘 수행할 수 있었죠. 이 뿐만 아니라, 별도의 튜닝 없이도 프롬프트만으로도 문제를 해결하는 능력이 매우 뛰어났기 때문에 Decoder-Only 모델이 대세가 되었습니다.
하지만, 이 방식은 딱 봐도 연산량이 어마어마할 것 같은데 이런 엄청난 연산을 그냥 냅둘 수는 없었으니...
그래서 등장한게 바로 KV Cache로 중복된 계산 결과를 메모리에 저장하고 있는 것입니다.
이에 대해서는 아래의 링크에 잘 정리되어있으니 참고해주시면 될 것 같습니다!
https://coding-review.tistory.com/613
기술 발전 순서로 알아보는 KV Cache
안녕하세요, 이번엔 KV Cache에 대해서 공부해본 내용을 포스팅으로 정리해볼까 합니다. 요즘 AI 엔지니어링을 하면서 가장 고려해야하는 것이 바로 이 KV Cache가 점유하게되는 메모리를 관리하는
coding-review.tistory.com
마치며
이번 포스팅에서는 Transformer가 태동할 때부터 있었던 근본 개념들인 Attention, 위치 정보 벡터, Encoder와 Decoder에 대해서 공부해보고 정리해봤습니다.
이번 포스팅을 쓰면서 궁금한 것들이 마구마구 쏟아졌는데 바로 다음 포스팅으로 뉴럴 링크와 역전파를 쓸지... 아니면 어떻게 페르소나를 주입하면 그대로 행동하게 되는지 프롬프트 엔지니어링의 동작 방식을 쓸지... 둘 다 쓰긴 할거지만 오랜만에 포스팅을 쓰니 쓸 내용이 너무 많네요.
일단 이번 포스팅을 통해서 Transformer의 동작 방식에 대해서 깊이있게 공부해볼 수 있는 좋은 기회가 되었습니다.
이번 포스팅은 여기서 마치도록 하겠습니다. 긴 글 읽어주셔서 감사합니다. 오늘도 즐거운 하루 되세요!
'AI Engineering > 이론' 카테고리의 다른 글
| LLM한테 페르소나를 적용하면 어떻게 이를 수행하는걸까? (0) | 2026.01.24 |
|---|---|
| 기술 발전 순서로 알아보는 KV Cache (0) | 2026.01.21 |
| 특명: 추론 속도를 올리기 위한 온몸 비틀기 (Speculative Decoding) (0) | 2026.01.19 |
| vLLM은 어떻게 AI 엔지니어링에서 필수불가결한 선택지가 되었을까? (0) | 2026.01.08 |
| 양자화란 무엇인가 (0) | 2025.12.09 |