작년 12월쯤에 데이터베이스 인덱스에 관한 포스팅을 진행한 적이 있습니다. 하지만 그때 당시 제대로 된 문서를 찾아보고 포스팅을 한 것이 아니라 다른 분들이 블로그에 올리신걸 짜집기 해서 적은 것이라 내용이 많이 부실합니다.
이번 포스팅에서는 이전 인덱스에 관한 내용을 리뉴얼하는 과정을 거칠 것이고 그렇기 때문에 이번 포스팅은 꽤나 알차게 작성할 예정입니다.
각설하고 시작해보죠
인덱스

우선 이런 데이터가 있다고 가정해봅시다. 이 상태에서 점수가 30점인 학생을 찾고 싶습니다. SQL문 SELECT 어쩌구 해서 만들겠죠?
SQL문을 그렇게 만들면 데이터를 가져올겁니다. 하지만 기존 DBMS는 데이터를 검색할 때 모든 데이터를 다 뒤져서 가져옵니다. 점수가 30점인 학생을 찾기 위해서 다섯개의 레코드를 다 뒤져본다는 얘기죠.
그럼 만약 데이터가 다섯개가 아니고 1억개면 어떻게 할까요? 맞습니다. 30점인 학생을 찾기 위해 1억건의 데이터를 전부 확인할 것입니다.
이건 아무리 봐도 문제가 있죠. 여기서 인덱스라는게 등장합니다.
숫자 찾기
1부터 100까지 적혀있는 카드가 있고 제가 숫자 하나를 임의로 선택해 생각하고 있도록 하겠습니다. 여러분은 제가 생각한 숫자를 찾는 것입니다.
기존 컴퓨터가 제 숫자를 찾기 위해서는 이렇게 접근할 것입니다.
- 생각하신 숫자가 1입니까?
- 생각하신 숫자가 2입니까?
- 생각하신 숫자가 3입니까?
- 생각하신 숫자가 4입니까?
- (.....)
하지만 자료구조, 알고리즘을 조금 아시는 분들은 이렇게 대답할 것입니다. 그거 '이진 탐색 트리' 쓰면 간단하잖아?
이진 탐색 트리에 대해서 자세히 알고싶으신 분들은 아래의 링크를 확인해주세요. 이진 탐색 트리에 대한 내용은 본 포스팅과 어울리지 않아 생략하도록 하겠습니다.
https://coding-review.tistory.com/286
자료구조 : Tree
이번 시간에는 전 시간에 이어서 컴퓨터 사이언스에서 가장 사랑받는 자료구조 중 하나인 Tree에 대해서 알아보도록 하겠습니다. 이번 포스팅에서는 Tree의 개념, Tree 구조에서 가장 많이 사용하
coding-review.tistory.com
방금 위와 같은 방법으로 찾으면 운이 안좋은 경우 100번을 물어봐야 원하는 답을 얻을 수 있었지만, 이진 탐색 트리를 활용한다면 8번만에 원하는 답을 얻을 것입니다.
- 50보다 큽니까?
- 75보다 작습니까?
- 63보다 큽니까?
- (.....)
이렇게 반씩 줄여가다 보면 더 효율적으로 원하는 대답을 얻을 수 있겠죠. 이게 바로 인덱스가 사용하는 방식입니다.
하지만 앞선 숫자찾기 게임에서도 정렬이 된 카드들 중에서 반씩 나눠가면서 찾았죠? 그렇기 때문에 이렇게 효율적으로 찾기 위해서는 정렬이 필수입니다.

이렇게 정렬이 된 데이터만 갖고 있다면 이진 탐색 트리를 활용해 원하는 답을 빠르게 찾을 수 있을겁니다. 때문에 이렇게 정렬되어있는 데이터 값들을 '인덱스' 라고 부르는 것이죠.
여기서는 '점수' 컬럼이 인덱스가 되겠네요.
인덱스의 장점
인덱스의 장점은 뭐니뭐니해도 검색성능의 향상입니다. 저렇게 정렬을 시켜놓고 검색하면 시간복잡도가 O(n)에서 O(logn) 으로 획기적으로 줄일 수 있으니까요.
인덱스의 단점
이게 좀 치명적이라고 느끼실 수도 있습니다. 인덱스를 만들어 놓았을 때의 단점은 크게 두가지입니다.
우선 삽입, 수정, 삭제를 하고 싶은 경우 인덱스에도 똑같은 작업을 해줘야겠죠. 원본 데이터와의 일관성을 유지해야하니까요. 그렇기 때문에 검색 성능보다는 조금 떨어지는 성능을 보여줍니다. 하지만 요즘은 연산속도가 워낙 빨라져서 딱히 걱정할 필요는 아니라고 하네요.
다음으로 인덱스를 관리할 저장공간이 필요하다는 것입니다. 만약 인덱스를 사용하고싶다면 데이터베이스 전체 저장소의 10퍼센트 정도 되는 하드웨어 저장소가 필요합니다.
그렇기 때문에 우리는 인덱스를 좀 더 신경써서 만들 필요가 있습니다. 더 효율적이고 더 빠르게말이죠. 그렇게 고대의 개발자분들께서 획기적인 데이터 구조를 만들어내셨습니다. 바로 B- tree입니다.
B- tree
읽을 때는 B- tree (비 마이너스 트리) 라고 읽으면 됩니다. 이 B- tree는 데이터베이스 성능을 획기적으로 올려주는 데 탁월한 공헌을 한 데이터 구조입니다.
우선 어떻게 생겼는지부터 확인해보시죠.

우리가 알고있던 이진 탐색 트리와 조금 다르네요? 노드에 두개이상의 데이터가 들어가있습니다. 자 이렇게 두개 이상의 노드가 들어가게 되면 어떤일이 생길까요?
기존 이진 탐색 트리를 한번 보겠습니다.

데이터를 반씩 갈라가면서 찾는 방법이 바로 이진 탐색 트리였습니다. 때문에 이진 탐색 트리의 시간 복잡도는 O(log n) 더 정확히는 O(log2 n)입니다.
하지만 노드가 하나가 아닌 두개 이상의 데이터가 들어가면 어떻게 되죠? 만약 각 노드별로 두개씩 있다고 가정해봅시다.
그럼 두개씩 갈라가면서 찾는게 아니고 네개씩 없애면서 찾을 수 있겠네요? 이해하기 조금 까다로울테니 예시를 가지고 설명해보겠습니다.
기존 생각한 수 = 60
- 50보다 위입니까? => 네
- 75보다 아래입니까? => 네
- 63보다 아래입니까? => 네
- 56보다 아래입니까? => 아니요
- 59보다 위입니까? => 네
- 61.5보다 위입니까? => 아니요
- 60.5보다 위입니까? => 아니오
- 60

생각한 수 = 145
- 100보다 작습니까? => 아니요
- 100과 155 사이입니까? => 네
- 128보다 작습니까? => 아니요
- 128과 140 사이입니까? => 아니요 => 이때 140 이상인 것이 확정
- 145
이해를 돕기위해 간단한 예제로 선택했는데 이해가 되셨는지 모르겠네요. 아무튼 이런 방식으로 크게크게 자를 수 있기 때문에 O(log2 n) 보다 더 효율적인 O(log3 n) 혹은 O(log4 n) 이렇게 만들 수 있습니다.
자 여기까지만해도 이미 획기적으로 성능을 끌어올렸습니다. 하지만 고대의 개발자들은 여기서 멈추지 않았습니다. 성능이 더 뛰어나고 더 효율적인 데이터 구조를 만들기 이르렀습니다. 바로 B+ tree 입니다.
B+ tree
읽을 때는 B+ tree (비 플러스 트리) 라고 읽으시면 됩니다.
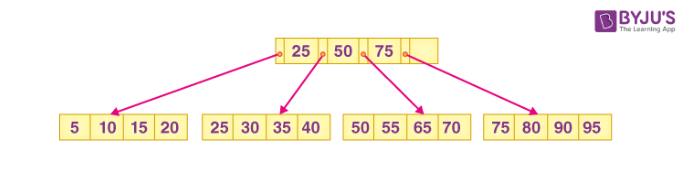
우선 B+ tree의 생김새부터 보고 가시죠.

기본적인 구조는 B- tree와 비슷한 것 같습니다. 뭔가 달라진게 있다면 맨 아래 화살표가 생겼다는 것 정도입니다.
위의 자료구조 Tree의 포스팅을 보시면 알겠지만 트리 구조는 크게 세가지로 나뉩니다.
맨위 = 루트 노드
중간 = 인터널 노드
맨아래 = 리프 노드
B+ tree의 가장 큰 특징은 모든 데이터가 리프 노드에 들어가있고 루트 노드와 인터널 노드에는 데이터가 직접 들어가지 않고 조건식만 들어가있습니다.
그렇기 때문에 트리의 높이를 B- tree 에서 한번 더 줄일 수 있었으며 모든 데이터가 리프 노드에 들어가 있기 때문에 검색 성능이 기존 B- tree 보다 더 빨라졌습니다.

위 그림은 B+ tree의 데이터 구조입니다. 조건문이 들어있는 인터널 노드에는 각각의 조건 사이에 자신이 어디위치로 가야하는지에 대한 레퍼런스가 적혀있습니다.
이를 통해 데이터베이스에서 데이터를 찾기 위해 어디로 가야하는지에 대한 방향을 알려주죠. 리프 노드끼리 화살표로 연결된 것은 모든 데이터가 리프 노드에 모여있기 때문에 다음 리프 노드로 넘어가기 위해서 부모 노드를 거치지 않고 바로 옆 리프 노드로 넘어가기 쉽게 하기 위해 만들어진 구조입니다.
이를 통해 범위를 설정했을 경우 뛰어난 성능을 보여줍니다. 만약 위의 예제에서 A 부터 E 까지를 원한다면 화살표를 따라 A서부터 E까지 흐름에 따라 이동하면 되기 때문에 성능상 더 뛰어난 강점을 가지고 있는 것입니다.
B+ tree에서의 검색

만약 위와 같은 B+ tree가 있다고 가정해보고 제가 원하는 데이터는 55라고 가정해보겠습니다. 제가 55에 가길 원한다면 결과적으로 50과 75 사이에 리다이렉트 되고 거기서 55를 얻을 수 있을 것입니다.
B+ tree에서의 삽입

방금과 같은 예제에서 제가 60이라는 데이터를 넣고 싶습니다. 하지만 리프 노드가 꽉 찼군요. B+ tree 는 이럴 때 리프를 쪼개는 작업을 진행합니다.
60이 들어옴으로써 50, 55, 60, 65, 70이라는 리프 노드가 가운뎃값을 기준으로 쪼개집니다. 즉 (50, 55) / (60, 65, 70) 이렇게 쪼개지는 것이지요.

B+ tree 에서의 삭제
만약 다시 60이라는 숫자를 삭제하고싶다고 가정해보겠습니다. 그럼 우리는 리프 노드를 합쳐야할 필요가 생깁니다. 물론 그대로 놔두는 것도 좋겠지만 그 위의 부모노드가 점점 더 비대해지게 될 것이고 이는 성능상 악영향을 미칠 것입니다.
그렇기 때문에 이렇게 합쳐진 B+ tree 를 볼 수 있습니다.
마치며
여기까지 데이터베이스 인덱스, 그리고 인덱스의 자료구조인 B- tree, B+ tree 까지 알아봤습니다. 인덱스는 이해하기 좀 쉬운데 자료구조는 이해하기 좀 까다로워서 문서를 보면서도 어떻게 정리해야할지 많이 고민했던 것 같습니다.
만약 인덱스와 B- tree, B+ tree를 알기위해 들어온 분들이 좀 더 쉽게 이해하셨으면 하는 마음에 깊은 내용보다는 간추려서 포스팅을 작성했습니다. 긴 글 읽어주셔서 감사합니다. 오늘도 즐거운 하루 되세요~
참조
https://dev.mysql.com/doc/refman/8.0/en/mysql-indexes.html
MySQL :: MySQL 8.0 Reference Manual :: 8.3.1 How MySQL Uses Indexes
8.3.1 How MySQL Uses Indexes Indexes are used to find rows with specific column values quickly. Without an index, MySQL must begin with the first row and then read through the entire table to find the relevant rows. The larger the table, the more this cos
dev.mysql.com
https://www.scaler.com/topics/b-tree-in-dbms/
B Tree in DBMS | Scaler Topics
Learn the concept of B Tree in DBMS with Scaler Topics.
www.scaler.com
https://byjus.com/gate/b-plus-tree-in-dbms-notes/
B+ Tree in DBMS | GATE Notes
B+ Tree in DBMS: B+ Tree is a B Tree enhancement that enables faster insertion, deletion, and search operations. Visit to learn more about B+ Tree.
byjus.com
'CS 지식 > 데이터베이스' 카테고리의 다른 글
| Redis를 이용해 캐싱 구현하기 (with Spring) (0) | 2023.05.03 |
|---|---|
| Redis의 기초적인 개념 (0) | 2023.05.03 |
| NoSQL의 BASE속성으로 인한 단점은 단점이 아니다 (0) | 2023.03.22 |
| Elasticsearch (0) | 2023.03.17 |
| CAP 정리와 한계 PACELC 정리 (0) | 2023.03.12 |